セキュリティの世界において、最大の革命の一つと言われるのが「公開鍵暗号方式」の発明です。
前回学んだ「共通鍵暗号」には、「鍵を相手に送らなければならないが、送る途中で盗まれたら終わり」というジレンマ(鍵配送問題)がありました。これを魔法のように解決したのが公開鍵暗号です。
しかし、その仕組みを理解しようとすると、「素因数分解」や「楕円曲線」といった難解な数学の壁が立ちはだかります。ここで挫折してしまう方も多いのではないでしょうか。
安心してください。SC試験対策として必要なのは、複雑な計算ができることではありません。「どんな数学的な性質を利用して、なぜ安全だと言えるのか」というイメージを掴むことです。
今日は、公開鍵暗号の代表格であるRSAとECC(楕円曲線暗号)について、数式は極力使わず、その「数学的な仕掛け」を直感的に解説します。
公開鍵暗号の基本アイデア「2つの鍵」
共通鍵の悩みを解決する逆転の発想
共通鍵暗号が「家の鍵(開け閉めが同じ鍵)」だとしたら、公開鍵暗号は「南京錠」のようなものです。
想像してみてください。あなたは遠くの友人に秘密の手紙を送りたいとします。
- まず、友人から「開いた状態の南京錠(公開鍵)」だけを送ってもらいます(鍵本体は友人が持ったままです)
- あなたはその南京錠を使って、手紙を入れた箱に鍵をかけます(暗号化)
- 鍵のかかった箱を友人に送ります
この箱は、南京錠をかけたあなた自身でさえ開けることはできません。開けられるのは、その南京錠の「鍵本体(秘密鍵)」を持っている友人だけです。
「公開鍵」と「秘密鍵」の役割分担
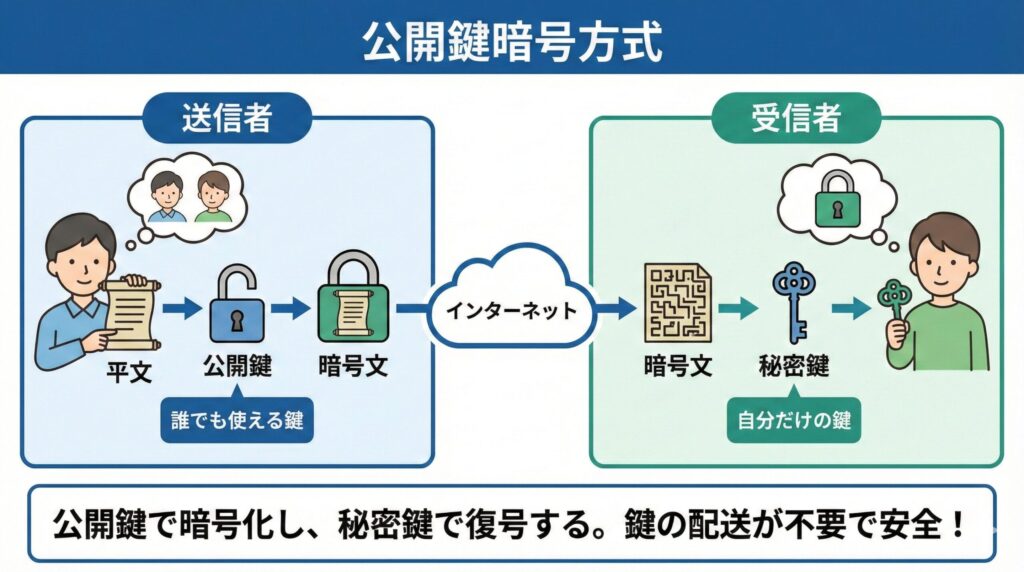
公開鍵暗号方式では、ペアとなる2つの鍵を使います。
公開鍵(Public Key):
- 役割: データを「暗号化」するための鍵。南京錠そのもの
- 扱い: 名前通り、世界中に「公開」してOK。誰に盗まれても問題ありません
秘密鍵(Private Key):
- 役割: 暗号文を「復号」するための鍵。南京錠を開ける鍵本体
- 扱い: 自分専用。絶対に他人に見せてはいけません
「誰でも暗号化できるけれど、復号できるのは持ち主だけ」という非対称な関係を作るのがポイントです。このため、公開鍵暗号は「非対称鍵暗号」とも呼ばれます。
なぜこれで「鍵配送問題」が解決するの?
答えはシンプルです。「守るべき秘密の鍵を、配送していないから」です。
ネットワークを通じて相手に送るのは「公開鍵(盗まれても良い鍵)」だけです。一番大事な「秘密鍵」は、作成した本人の手元から一歩も外に出ません。
例えば、オンラインショッピングの場合を考えてみましょう。Amazonのような大手サイトは、自分の公開鍵を世界中のユーザーに配布しています(Webブラウザが自動的に取得します)。あなたがクレジットカード番号を入力すると、その情報はAmazonの公開鍵で暗号化されて送信されます。途中で誰かに盗聴されても、暗号文しか見えません。そして、その暗号文を復号できるのは、Amazonが厳重に管理している秘密鍵だけです。
これにより、共通鍵暗号の最大の弱点であった「鍵を安全に送る方法がない」という問題が根本的に解決したのです。
公開鍵暗号の処理速度という課題
ただし、公開鍵暗号にも弱点があります。それは「処理速度が非常に遅い」ことです。共通鍵暗号と比べて、数百倍から数千倍も時間がかかります。
そのため、実際のシステムでは「公開鍵暗号で共通鍵を安全に交換し、本体のデータは共通鍵暗号で暗号化する」というハイブリッド方式が使われています。これについては次回詳しく解説します。
RSA暗号の仕組み(素因数分解の壁)
安全性の根拠は「計算の難しさ」
では、どうやって「暗号化は簡単だけど、復号は難しい」という状況を作っているのでしょうか。ここで数学の出番です。
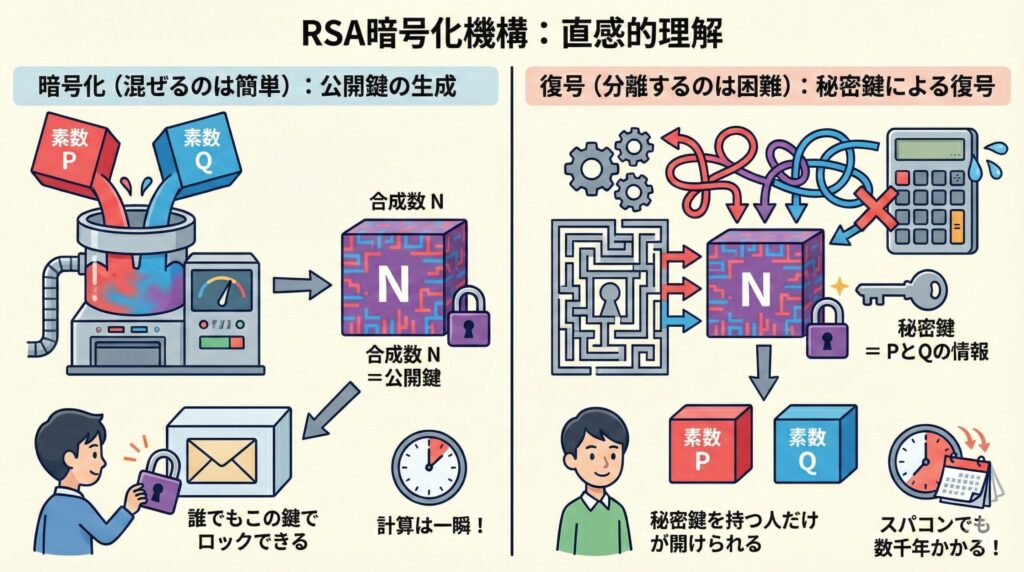
現在最も有名な公開鍵暗号であるRSA暗号は、「大きな数の素因数分解は非常に難しい」という数学的な性質を利用しています。
RSAという名前は、開発者であるRivest、Shamir、Adlemanの3人の頭文字から付けられました。1977年に発表されて以来、40年以上にわたってインターネットセキュリティの基盤を支えてきた歴史ある暗号方式です。
「掛けるのは簡単、戻すのは困難」
直感的なイメージで説明します。
絵の具を想像してください。「赤」と「青」の絵の具を混ぜて「紫」を作るのは一瞬で簡単にできます(掛け算)。しかし、出来上がった「紫」の絵の具を見て、「これを元の赤と青に完全に分離してください」と言われたらどうでしょうか?これは非常に困難です(素因数分解)。
RSA暗号では、これと同じことを数字で行います。
- 2つの巨大な素数(例えば数百桁の数)を掛け合わせて、さらに巨大な数(N)を作るのは、コンピュータなら一瞬です
- しかし、その巨大な数(N)だけを見て、「どの素数同士を掛けたのか?」を割り出す(素因数分解する)には、現在のスーパーコンピュータでも数年から数万年かかると言われています
この「元に戻す(復号する)ことの圧倒的な難しさ」が、RSA暗号の安全性の盾となっています。
素数とは何か?
補足として、「素数」について簡単に説明しておきます。素数とは、1とその数自身以外では割り切れない数のことです。例えば、2、3、5、7、11、13などです。4は2で割り切れるので素数ではありません。
小さな数では素数を見つけるのは簡単ですが、数百桁の巨大な素数を見つけるのは、それだけでも大変な計算です。そして、その巨大な素数2つを掛け合わせた数を元の2つの素数に分解するのは、さらに困難なのです。
RSA暗号の現状と未来
RSAは長年セキュリティの主役でしたが、コンピュータの性能向上に伴い、安全性を保つために必要な鍵の長さ(ビット数)がどんどん長くなってきています。現在は2048ビット以上が推奨されており、より高度なセキュリティが求められる場合は4096ビットが使われることもあります。鍵が長くなると、その分計算処理も重くなります。
また、遠い将来「量子コンピュータ」が実用化されると、素因数分解が簡単に解けてしまう可能性が指摘されています。量子コンピュータは、従来のコンピュータとは全く異なる原理で動作し、特定の種類の計算を劇的に高速化できるとされています。このため、次世代の「耐量子計算機暗号」の研究も世界中で進められています。
ECC(楕円曲線暗号)の仕組み(新しい数学の力)
RSAより「短くて強い」次世代のエース
RSAに代わって、現在主流になりつつあるのがECC(Elliptic Curve Cryptography:楕円曲線暗号)です。
ECCの最大のメリットは、「RSAよりも短い鍵長で、同等の安全性を確保できる」ことです。例えば、RSAの2048ビットと同じ強度を、ECCならわずか224ビット程度で実現できます。
鍵が短いということは、計算が速く、通信データ量も少なく済むことを意味します。そのため、処理能力が限られるスマートフォンやIoT機器での利用に非常に適しています。バッテリー消費も少なく抑えられるため、モバイル環境では特に有利です。
楕円曲線ってなに?(イメージで掴む)
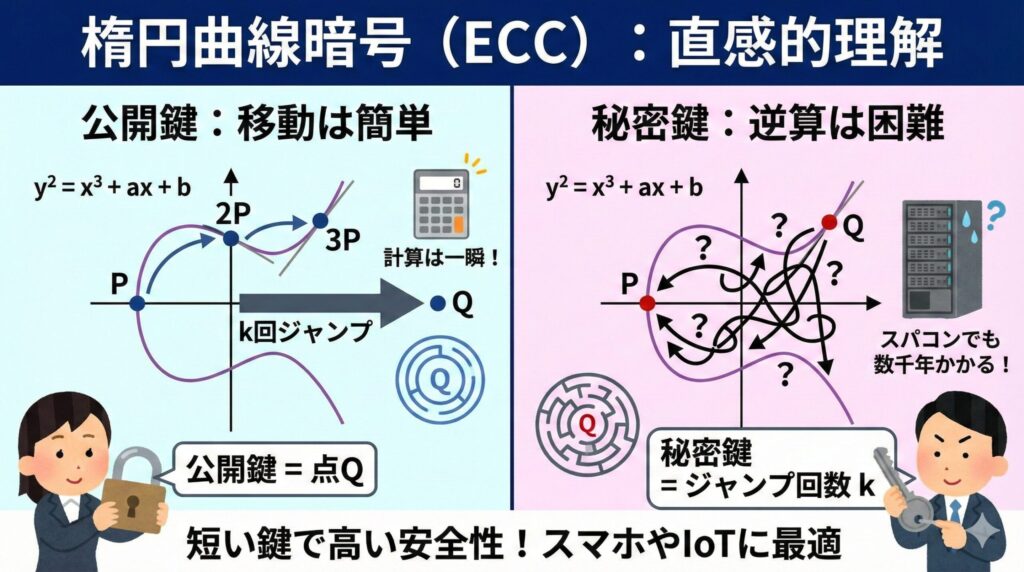
ECCは「楕円曲線」という複雑なグラフ上の点の性質を利用しますが、その仕組みを直感的に言うと「グラフ上のすごろくゲーム」のようなものです。
- 特殊な形のグラフ上にスタート地点の点(P)を置きます
- あるルールに従って、グラフ上を「点P → 点2P → 点3P…」とジャンプ(移動)していきます
- これを「秘密の回数(例えば1億回)」繰り返して、ゴール地点の点(Q)に到達します
この時、次のような特徴があります。
- スタート点(P)とジャンプ回数から、ゴール点(Q)を計算するのは簡単です(暗号化)
- しかし、スタート点(P)とゴール点(Q)だけを見て、「何回ジャンプしたか?」を逆算するのは非常に困難です
これが「楕円曲線上の離散対数問題」と呼ばれる難問です。この「逆算の難しさ」を安全性の根拠としています。RSAの素因数分解よりも、さらに解くのが難しい問題を利用しているため、短い鍵でも安全なのです。
なぜ「楕円曲線」と呼ぶのか?
「楕円曲線」という名前から、楕円形を想像するかもしれませんが、実際にはもっと複雑な曲線です。数学的には「y² = x³ + ax + b」という形の方程式で表される曲線のことを指します。この曲線が持つ独特な性質(点の加法と呼ばれる特殊な演算)が、暗号技術に利用されています。
身近な利用シーン
ECCはその効率の良さから、現代のインターネットを支える多くの場所で使われています。
Webサイトのセキュリティ(SSL/TLS): ブラウザのアドレスバーに鍵マークがついている通信(HTTPS)の多くでECCが使われています。Google、Facebook、Amazonなどの大手サイトは、すでにECCを標準的に採用しています。
ビットコイン(ブロックチェーン): 仮想通貨ビットコインでは、所有者の署名などにECCの技術(具体的にはsecp256k1という楕円曲線)が使われています。
スマートフォンのアプリ: LINEやWhatsAppなどのメッセージングアプリでも、エンドツーエンド暗号化にECCが使われています。
RSAとECCの使い分け
現在のシステムでは、RSAとECCが併存しています。RSAは歴史が長く、多くのシステムで実装されているため、互換性の観点から引き続き使われています。一方、新しいシステムや、処理能力が限られるモバイル環境では、ECCが選ばれることが多くなっています。
学んだ知識を定着させよう
ここまでの内容が、なんとなくイメージできたでしょうか? 「数式はわからなくても、安全性の理由が言える」状態がゴールです。理解度を確認するための簡単なクイズです。
【演習】公開鍵暗号方式(RSA, ECC)理解度チェック(全10問・詳細解説付き)
Q1. 公開鍵暗号方式における鍵の役割として、正しい組み合わせはどれか。
正解:イ
解説:
公開鍵暗号は「誰でも暗号化できる(公開鍵)が、復号できるのは本人だけ(秘密鍵)」という仕組みです。南京錠(公開鍵)と鍵本体(秘密鍵)の関係を思い出しましょう。
- ア:これは「デジタル署名」の仕組みです(本人が秘密鍵で署名し、他者が公開鍵で検証する)。暗号化通信とは逆になります。
- ウ・エ:同じ鍵を使うのは「共通鍵暗号方式」です。
Q2. 公開鍵と秘密鍵の管理方法として、適切な記述はどれか。
正解:ア
解説:
その名の通り、「公開鍵」は誰に知られても問題ありません。「秘密鍵」は復号に必要なため、絶対に他人に知られてはいけません。
- イ・ウ:秘密鍵を公開してしまったら、誰でも暗号文を復号できてしまい、暗号の意味がなくなります。
- エ:公開鍵を誰にも渡さないと、誰もあなた宛てのデータを暗号化できなくなります。
Q3. 公開鍵暗号方式の導入によって解決された、共通鍵暗号方式の最大の課題は何か。
正解:ウ
解説:
公開鍵暗号は「守るべき秘密鍵を配送しない」ことで、共通鍵暗号の最大の弱点であった「鍵配送問題」を解決しました。
- ア・イ:これらはむしろ公開鍵暗号のデメリット(共通鍵と比較して遅い、計算コストが高い)です。
- エ:現在の主要な公開鍵暗号(RSA, ECC)は、将来的に量子コンピュータで解読されるリスクが指摘されています(解決されていません)。
Q4. RSA暗号の安全性の根拠となっている、数学的な「計算の困難性」はどれか。
正解:ア
解説:
RSA暗号は、「大きな素数同士を掛けるのは簡単だが、その結果(合成数)を元の素数に分解する(素因数分解)のは非常に困難である」という性質を利用しています。
- イ(離散対数問題):これはECC(楕円曲線暗号)などの安全性の根拠です。
- ウ・エ:これらも数学的に困難な問題ですが、RSA暗号の根拠ではありません。
Q5. RSA暗号に関する記述として、適切なものはどれか。
正解:ウ
解説:
素因数分解の解読技術やコンピュータの計算能力が向上しているため、RSAで十分な安全性を確保するための鍵長は年々長くなっています(現在は2048ビット以上が推奨)。
- ア:RSAは公開鍵暗号であり、共通鍵暗号より処理は低速です。
- イ:同等の安全性で比較すると、RSAの方がECCより鍵長はずっと長くなります。
- エ:鍵長が長く計算負荷が高いため、リソースが限られた環境にはECCの方が適しています。
Q6. ECC(楕円曲線暗号)の安全性の根拠となっている数学的な問題はどれか。
正解:イ
解説:
ECCは、楕円曲線上の点に定義された演算において、「ある点から何回移動してゴールに到達したか(離散対数)を逆算するのは困難である」という性質を利用しています。
- ア(素因数分解):これはRSA暗号の根拠です。
- ウ(ハッシュ衝突):ハッシュ関数の安全性に関わる問題です。
- エ:素数判定などに使われる定理ですが、ECCの直接の根拠ではありません。
Q7. ECC(楕円曲線暗号)がRSAと比較して優れている点(メリット)はどれか。
正解:イ
解説:
これがECC最大のメリットです。例えば、RSAの2048ビットと同等の強度が、ECCでは224ビット程度で実現できるとされています。
- ア:楕円曲線の数学は、素因数分解(RSA)よりも複雑で理解が難しいとされています。
- ウ:歴史が長く標準的に広く使われてきたのはRSAです(ECCは比較的新しい)。
- エ:ECCは公開鍵暗号の中では効率的ですが、AESなどの共通鍵暗号よりは低速です。
Q8. ECC(楕円曲線暗号)の特徴から、特に利用に適している環境はどれか。
正解:ア
解説:
ECCは鍵長が短く、計算負荷や通信データ量を抑えられるため、リソースの限られたモバイル端末やIoTデバイスでの利用に非常に適しています。
- イ:使えないわけではありませんが、ECCの「効率性」というメリットが最も活きる環境ではありません。
- ウ:大容量データの高速暗号化には、AESなどの「共通鍵暗号」が適しています。
- エ:現在のECCはRSAと同様に、量子コンピュータによって解読されるリスクがあります(耐量子暗号ではありません)。
Q9. 一般的な傾向として、公開鍵暗号方式と共通鍵暗号方式の処理速度を比較した場合、正しい記述はどれか。
正解:イ
解説:
公開鍵暗号は複雑な数学的計算を必要とするため、単純なビット演算などが中心の共通鍵暗号と比較して、処理速度は数百倍〜千倍程度遅くなるのが一般的です。
- ア・ウ・エ:仕組みの複雑さが全く異なるため、一般的に共通鍵暗号の方がはるかに高速です。
Q10. 実際のインターネット通信(SSL/TLSなど)では、公開鍵暗号と共通鍵暗号を組み合わせた「ハイブリッド暗号方式」が用いられることが多い。この方式において、公開鍵暗号は主にどのような目的で使われるか。
正解:ウ
解説:
「遅いが鍵配送ができる公開鍵暗号」で、データ暗号化用の「速い共通鍵」を包んで送る。これがハイブリッド暗号の核心であり、公開鍵暗号の主要な役割です。
- ア:全データの暗号化には、高速な共通鍵暗号が使われます。
- イ:ハッシュ計算にはハッシュ関数(SHA-256など)が使われます。
- エ:デジタル署名にも使われますが、「それだけ」ではありません。共通鍵の配送(鍵交換)も重要な役割です。
まとめ
今日は、少し難解な「公開鍵暗号方式」の数学的仕組みについて、イメージ中心に解説しました。
- 公開鍵暗号の基本: 「暗号化する公開鍵」と「復号する秘密鍵」のペアを使う。これで鍵配送問題を解決した。
- RSA暗号: 「巨大な数の素因数分解は困難である」という性質を利用。歴史があるが、鍵が長くなりがち。
- ECC(楕円曲線暗号): 「グラフ上の点の移動回数を逆算するのは困難(離散対数問題)」という性質を利用。短くて強い、現代の主流。
ここまで、共通鍵と公開鍵、2つの暗号方式を学んできました。
「共通鍵は速いけど、鍵を渡せない(鍵配送問題)」
「公開鍵は鍵を渡せるけど、処理が遅い」
それぞれの長所と短所が見えてきたと思います。
では、実際のインターネット通信(SSL/TLSなど)では、どうしているのでしょうか?実は、「共通鍵の速さ」と「公開鍵の便利さ」をいいとこ取りした方法を使っているのです。
次回は、その巧妙な仕組みである「ハイブリッド暗号方式」について解説します。ここまでの知識がパズルのように組み合わさる、暗号技術のクライマックスです。どうぞお楽しみに!